1I would like to approach Giovanni Piana’s philosophical investigations from a marginal perspective, that is from our common passion for geometry. After all, he embodied the possibility of rethinking a problem without feeling too much the weight of age-old debates and letting unnoticed sentences reveal unexpected ways. “How strange this statement is”, he used to start like this, from a trifle, and then climb the dizzy path of pure thought.
2Geometry is bound up with figures, but also with space. Piana was always fascinated by space, because of the paradigmatic way empirical and logical aspects mix in this “bastard concept”,1 giving rise to “complex dialectics between experience and conceptual formations” (NF 106). Piana started from a plain assumption: space, and not only time, is a process—arguing against the dichotomy which assumed static space versus dynamic time.2 This idea reverberates in geometry and, against a naïve conception of geometry, it becomes essential to underline the genesis of geometrical figures. It is no coincidence that he particularly loved conical sections, the curves of Kock and the fractal geometry of Mandelbrot: shapes in motion.
3What I want to outline in this paper is that the dawn of the now widespread concept of diagrammatic reasoning, based on the grammar of space and on the discovery of the normativity of topological aspects, already lies behind Piana’s analysis of the givenness of geometrical figures.3 We can find it, in a nutshell, in the second part of Piana’s book Numero e Figura. Idee per una epi|stemologia della ripetizione entitled: ‘Sulla costruzione iterativa delle figure’. Piana’s emphasis is on the ‘iterative’ aspects—hence the ideas of repetition, of algorithm, and of etceteration—and on the ‘generative’ process displayed by the grammar of the figures themselves. Three important points are developed in the background: first, the outlining of a “logic of figures” (NF 123-127) as distinct from a ‘logic of propositions’—that is to say, the “meaning woven into the figure” (NF 122) and the “transparency of structure” (NF 176); secondly, connected to this peculiar ‘logic,’ the idea of “possible dynamisms of perception” (NF 122) and that of the “generative link” (NF 103); and thirdly, the already mentioned “complex dialectics between experience and conceptual formations” (NF 102).
1 | Number and Figure and the beginning of geometry
4Piana’s Euclid will give his hand to Mandelbrot, on the one side, and to sense experience, on the other, in fact, “Greek geometry did not spring from Euclid’s head, like Minerva from Jupiter’s” (NF 99). Starting from experienced spatiality, Euclidean geometry gave rise to a language game that advances the claim to go beyond experiential data but, however, maintains a relation with them. Instead, non-Euclidean geometry is said not to have a semantics that can be linked to experience (Piana would later change his mind, acknowledging unexpected links to experienced spatiality also in Lobačevskij’s geometry).4
5Despite being different from intuitive spatiality, Euclidean geometrical space is a logical artefact which stems through idealization (and not via abstraction)5 from given perceptual space. To achieve this, in the very first constituents6 of geometry the language should be twofold, appealing to both worlds, the intuitive and the conceptual. The first geometrical definitions, in fact, as Piana explains, “straddle very different language games” (NF 107). For instance, in the following definition: “A line is breadthless length” (Euclid 1956, 153), two different language games tend partially to superimpose on each other, by “referring to the thickness of a line, even if only to exclude it” (NF 107). Like Janus, “that sentence looks from two sides, on the one hand towards the concreteness of the experienced line, on the other to the line as an idea, to the abstract-geometrical concept of the line” (NF 107). Without relying on intuition, geometry must in any case ensure that the link between empirical and geometrical space is maintained. The concept of the straight line, in fact, is reached through idealization (actually, via ‘passage to the limit’): what is at stake here are “processes of departure from the world of experience” (NF 120). The term Piana appeals to, in describing this process, is a German one, to be exact Hegelian: “And all this [the everyday language] must be overcome and suppressed. But this Aufhebung is a complicated process, in a way always started and never finished” (NF 106-107).
6And here is why he can speak in this case of ‘dialectics between language-games’: “All the attention is devoted to the idea of an experienced spatiality from which the idealization processes start” (NF 120).7 This is the occasion, for Piana, for a little criticism of Kant: “[H]is aesthetic fails the phenomenological tasks of an authentic philosophy of experience, precisely because from the very beginning Kant’s theory targeted the possibility of objective knowledge” (NF 120). Piana’s fundamental idea that objective knowledge should not be separated from experience is the basis for grounding geometric idealization on the rules of experienced spatiality and not being abstracted from them in the direction of conventionality and arbitrariness.
7More than general idealizations, we find in geometry a sort of “iterative action [azione iterata]” (NF 101) directed by a rule: Euclidean postulates are an instance of this. The first one prescribes (against expectations in ordinary life) the absolute possibility of drawing a straight line from any point to any point. Behind this prescription we have the constructive vein of Euclidean geometry and with it the splendid definition of postulates that Piana has given us: an “ontologically productive action” which formulates “one of the conditions that brings about [pone in essere] certain objects, be they lines or circles” (NF 115). This postulate connects the operative iteration with infinity: “we begin therefore to identify the notions of order, of iteration and of proceeding-toward-a-limit as some of the levers on which thought can rest in its production of new objectivities” (NF 101).
8Despite the initial straddling of two languages, Piana can finally emphasize the explicit break made by Euclid: “[I]n Euclid, a totally new model of discourse, and one never experimented before him, is inaugurated. What is invented is a real new language game” (NF 99).
2 | The ‘logic of figures’ and the ‘transparency of structure’
9But looking carefully, another Euclidean revolution seems to come forth: “There is a logic of figures: this is a point of particular importance. Geometry arises from the thought of making this logic explicit, a logic with which, therefore, it has to do above all” (NF 123). Hence, the task of this paper is to follow this peculiar logic—made of lines, structures and internal links emerging at the level of the figure—in alternative to the other logic, i.e. the logic of propositions—made of words and, therefore, representing an axiomatic-formal point of view.8
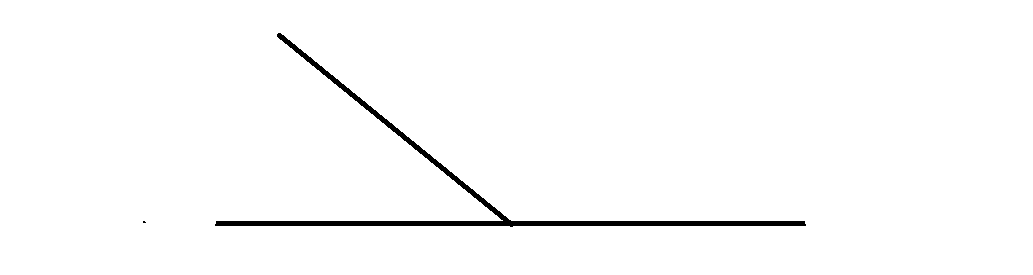
10Also, the logic of figures is not necessarily immediate, and it requires further connections. In Number and Figure, Piana’s goal is to grasp the constructive algorithm behind figures. He focuses on the iterative cases (Mandelbrot and Koch), but this constructive procedure can be valid in general, such as the prescription of constructing an equilateral triangle from two intersecting circles. Furthermore, with the keyword of ‘iteration’ he solves two aporias in one shot: first, he can explain the process of idealization at the basis of Euclidean geometry, without falling into a ‘too elementary epistemology’, victim of prejudices (either the intuitionist or the logicist);9 secondly, he captures the figure as a moment within a process: “the figure is not conceived in itself, in isolation and statically, but as a moment within a process” (NF 104).
11In this way, in fact, a geometrical figure is more an operative rule than something fully given: “we have already noticed that, in any case, here we go a little beyond what we ‘literally’ see” (NF 121). For instance, in the way we can consider the possible variation of the inclination of adjacent and complementary angles, we know that “varying the acute angle will impact the variation of the obtuse one, according to a specific rule: to a ‘more and more’ from one side, there must correspond a ‘less and less’ from the other” (NF 122).
12The givenness of the figure, therefore, hints at “the possible dynamisms of perception” (Piana, 1999, 122); however, this dynamism is not arbitrarily displayed by subjectivity but by the syntax of space and by the ‘logic of figure’:
This meaning is woven into the figure [intessuto nella figura] insofar as I grasp its structure and a possibility of variation in it. This possibility lies in the intentional folds of this grasp. The spatial form is sometimes wrongly indicated as a real ‘symbol’ of staticity. Instead, there is a way of looking at it that sets it in motion, it is-so in a being-becoming-other, according to coherent possibilities of variation and transformation (NF 122).10
13These “coherent possibilities of variation” are bound to an established range of variation easily grasped from spatial rules of coexistence: therefore, the idea of complementarity angles is given not by abstraction, but by a generative rule in space. The diagrammatic understanding of figures requires an intuition of the underlying constructive rule (which for Euclidean figures could be very simple), instead of ‘literally’ seeing a static figural perception. Elsewhere, Piana expresses himself as follows: the figure “is what it is, but at the same time we can say that it is in the way it is generated” (Piana 2015, 17). He can therefore state:
Construction is of interest in that it is capable of exhibiting internally justified steps, that is, which have their justification in the internal connections of the figure. The aim is to show these connections and to show them not as factually given, detected in the mere observation of the figure, but as links determined by the way in which the figure is generated, and therefore as links belonging to its essence (NF 110).
14The mere existence of something like a logic of figures (“the internal logic of figures”, NF 123) hints at contents organized according to rules intrinsic in the grammar of space, to connections inside the phenomenal material. The internal possibility of variation inside a class of figures is not unlimited (Piana speaks, in fact, of ‘coherent possibilities of variation’) and has its own laws:11 a figure arises from a process and its unity is given by the unity of the course [unità del percorso]. The appeal to a ‘logic of the figure’ is a fundamental step: thereby the discussion on the ‘characteristic aspect’ is abandoned in the name of a focus on the “display of a generative link [esibizione di un nesso generativo]”:
This rule consists of a modality of conceptual formation that cannot at all be described in the usual terms of the ‘common characters’ and of the relationship of genus to species, but rather consists in the display of a generative link, and therefore of a relationship that exists in strength of a possible path that leads, without gaps, from one object to another. In doing so, in reality, we also move away from a notion of conceptual formation that starts from the characteristic aspect (NF 103).12
15Let us consider now Piana’s dispute with Hans Hahn, which ends with Piana’s achievement of “the transparency of the structure which is presented in the constructive formula” (NF 176). Hahn wrote a paper, entitled ‘The Crisis in Intuition’,13 in order to show how often, in geometry, intuition has led us astray, and hence, to legitimate the demand for a complete formalization of mathematics and for the expulsion of intuition from mathematical reasoning, so that “propositions that had formerly been accepted as intuitively evident had to be painstakingly proved” (Hahn, 1980, 93). As an example of something contrary to intuition, both Hahn and Poincaré refer to the completely tangent-free curve devised by Weierstrass in 1861. With regard to this proposal, Hanh wrote: “The character of this curve entirely eludes intuition; indeed after a few repetitions of the segmenting process the evolving figure has grown so intricate that intuition can scarcely follow” (Hahn 1980, 84), and he adds: “the fact is that only thought, or logical analysis can pursue this strange object to its final form” (Hahn 1980, 84).
16Piana, on the other hand, patiently investigates the morphological genesis of Weierstrass curve, finding at its basis the repetition ad infinitum of a simple pattern. On the grounds of this movement ad infinitum, made possible by the thought of etceterability, it will therefore be possible to speak of a similar curve as a curve without tangents at all its points, without thereby countering intuition. What is at stake here is that the reference to the formula in the already quoted “transparency of the structure that is presented in the constructive formula” is not intended to be an attempt to algebraize geometry, but a hint at the internal constitution and articulation of the figure inside the grammar of space, against a static conception of shapes given once and forever. A case in point is the infinite Pythagorean starred pentagram and its recursive procedure, introduced by Piana via “a sign-generating algorithm” (NF 132)—i.e., a sort of ‘forward’ operation upon a completely syntactic element—in continuity with Euclid’s “iterated application of a rule” (NF 133) claimed by his postulates. Piana will detect that: “By adopting this point of view is the pentagon, and not the star, that has the character of outcome” (NF 154).
17But it is with the Koch curve (at the basis of fractal geometry) that this recursive method displays its greatest cogency: the final figural outcome might, in fact, conceal the operating scheme by which it is generated. Only by bringing to light the structure (here is the reason for the transparency of the structure), can we arrive at a complete conceptual understanding of the figure. This occurs not through the emphasis on the power of construction by the subject, but through the detecting of a generative link,14 tracing back the first elements of the given figure. As Proclus wrote in his Commentary on Euclid: “[…] and it is always the function of geometry,––either to construct figures or to compound or divide (διαιρέω) figures already constructed” (Proclus 1992, 32). In order to do that, we have to bring to light the logical character of space and, hence, the following relations: before and after, above and below, inside and outside, etc. But this perspective of discourse is entirely lacking in Hahn, in fact, as Piana recognizes: “it is we who speak of a logic of the figure. Hahn has no suspicion of it” (NF 177).15 And it is the diagrammatical plan which now comes to the fore exhibiting structural spatial laws.
The ‘co-exact’ properties and the ‘dynamism of perception’
18The claim that there exists a ‘logic’ inside figures is no small thing. According to Leibniz, the notion of space applies whenever it is a matter of combining multiple elements: at its root we find the idea of ‘syntax’, Σγνταχή, which is nothing but an order of coexistence.16 The already quoted “rule about the ‘more-and-more’ and ‘less-and-less’” is a perfect example of reciprocal ‘co-existence rules’, such as the notion of ‘configuration’ and of ‘characteristic development’. Without going so far as to embrace Friedrich Albert Lange’s radicalism (“it is sufficient to have shown that logic does not find firm ground except in the laws that arise from the consideration of space”),17 we can simply say that there is something like a “meaning woven into the figure” (NF 122) which arises from the structured perceived space and “is capable of exhibiting internally justified steps” (NF 110). What today is called ‘diagrammatical reasoning’ appeals to this same topological logic. As Piana observed:
In a perceived figurality, not only objects are grasped, but also structural relationships, internal formal connections, general laws that, on the one hand, are seen inside the figure, on the other, can be projected very far from it, onto the plane of pure thought (NF 85).
19There are internal articulations of lines which speak for themselves and offer general laws. They are capable of mirroring logical relations and offer an essential topological understanding of them through spatial relationships such as ‘betweenness’, ‘same-side-ness’, ‘under- or over-stayness’, ‘priority’ and ‘posteriority’: diagrammatic conditions which are insensitive to the effects of a range of variations in diagram entries. This is in tune with what Manders explained in his The Euclidean Diagram (Manders 2008). written in 1995 but not published until 2008 (it existed only as a draft for 13 years). Claiming the non-superfluous role of diagrammatic accounts, he prescribed a specific ‘diagram discipline’ in order to point out what demonstrations really do infer from diagrams and what they do not. Manders’ goal is to reconstruct the standards for producing and reading diagrams, in the belief that unwarranted generalization from the diagram is a danger fundamentally inherent in its mis-use.18
20Inside a figure, he outlines two different kinds of properties: 1. the exact and 2. the co-exact. With these terms, he means, respectively: quantitative features, on the one hand, and topological features, on the other. Manders’ prescription is to abstract from the particular (exact) features (e.g. specific lengths of sides and angles) and rely only on the features (co-exact) which are ‘unaffected by variation’. ‘Exact properties’, in fact, are the ones specific to a given case, whereas the co-exact are properties (e.g., the mere fact of an intersection, no matter at exactly what point) which are invariant across every possible deformation. Or, better, co-exact properties are “shared by a range of perturbed diagrams”, whereas “exact attributes are those which, for at least some continuous variation of the diagram, obtain only in isolated cases” (Manders 2008, 92). If exact attributes can be expressed by algebraic equations, co-exact attributes express “recognition of regions (and their lower-dimensional counterparts, segments and points) and their inclusion and contiguities in the diagram” (Manders 2008, 93).
21What counts here is that the grammar of space—or, in other words, the internal ‘logic of the figure’—is able to offer a range of contemplated variations.19 What Piana called “dynamisms of perception” or “seeing which is not mere seeing” or, again, “beyond what we ‘literally’ see” (NF 121), does not refer primarily to an introspective capacity of the mind, but to ‘passive synthesis’20 connected to a strict logic of the figure. Describing co-exact properties, Manders comes close to a phenomenological account: “co-exact attributes are those conditions which are unaffected by some range of every continuous variation of a specified diagram” (Manders 2008, 92). We face a sort of eidetic variation approach: “directly attributable features are ones with (a) certain perceptual cues that are (b) fairly stable across a range of variation of diagram (‘co-exact’ rather than ‘exact’) and (c) not readily eliminable by diagram discipline” (Manders 2008, 89). Manders speaks at this point of a “topology of a diagram,” meaning “the inclusions and contiguities of regions, segments, and points in the diagram” (Manders 2008, 89).21
22To contrast the claimed unreliability of assessments based on diagrams,22 Manders proposes a logical theory for Euclidean diagram-based reasoning which allows diagrams to contribute to proofs only through their co-exact properties. Exact conditions, in fact, “are unstable under perturbation of a diagram, therefore practice never allows an exact condition to be read off from the diagram” (NF 91). He can therefore speak of a ‘diagram discipline’ that is, a geometrical practice used to control the appearance of the diagram in order to avoid “fallacies of diagram use” (Manders 2008, 91).23 He explains how “traditional geometric demonstration has a verbal part” (i.e., ‘the discursive text’—what Piana calls ‘logic of propositions’), and “a graphic part” (the diagram—what Piana calls ‘logic of figures’) (Manders 2008, 86),24 and how those, diagram and text, contribute differently, proposing a sort of mixture of diagram- and discursive text-based moves.
23Typical gaps in Euclid, which “involve reading off some explicit co-exact feature from a diagram” (Manders 2008, 91), are therefore allowed: they express the topology of the diagram, i.e., the recognition of regions and their inclusions and contiguities. Manders is very scrupulous and he also proposes some stipulations in order to avoid any case in which the control by diagram has been lost; for instance, in the transition case where an intersection lies too far away to draw. What counts, here, is that the distinction between ‘exact’ and ‘co-exact’ attributes traces back to the genesis of the figure and to the reasons of its being.
24Geometrical constructions are in general only quasi-determinate and, in fact, in order to be shared by all figures of a given kind, co-exact attributes should be topologically invariant, that is to say, less determinate, whereas exact properties are always very specific. Mostly, co-exact features represent qualitative variables (to be inside, outside, intersected etc., without further specifications), whereas exact ones are quantitative features (specific dimensions, specific types inside their own genre and other idiosyncratic aspects). To explain this, I could resort to the chess-game (an example dear to Piana, such as to Husserl and Wittgenstein). Some moves, e.g. the bishop’s move, are described by a purely qualitative rule: ‘go diagonally’. In this case, the rule is ‘qualitative’ (no coincidence, that the two bishops are distinguished by a quality: the ‘white’ bishop and the ‘black’). The same applies to the tower: ‘always straight ahead’, with no quantitative prescription. Vice versa, the pawn’s move is basically quantitative: to move forward exactly by 1 (king’s and queen’s moves are a combination of the two). The bishop’s move (or the tower’s), never finds an exhaustive example: only all the moves together could be said to be an ‘exact’ projection of its possibilities, therefore it could be termed: ‘co-exact’. On the other hand, the single move of the pawn is basically quantitative and exact. The co-exact is therefore saved from the dictatorship of the omnimoda determinatio,25 without relapsing into the sphere of vagueness.
25We were already accustomed to considering geometrical figures in a particular way (for instance, disregarding performative imperfections); now we are required to take into consideration these topological distinctions, as well, and draw consequences from the invariant aspects only. But what is at stake here is not the psychological process concerning abstract ideas, but the topological plan, a specific “diagram discipline” (Manders 2008, 96-97) understood as an objective exercise that highlights internal rules based on the specific logic of the figure. Berkeley’s polemic about Locke’s definition of the ‘general idea of triangle’ (i.e. “neither oblique nor rectangle, neither equilateral, equicrural, nor scalenon, but all and none of these at once”) is well-known.26
26The psychological approach towards figures, instead, was widespread; in his Principles of Psychology, William James still describes the geometer’s attitude to figures as a capability of abstraction: “the geometer, with his one definite figure before him, knows perfectly that his thoughts apply to countless other figures as well, and that, although he sees lines of a certain special bigness, direction, colour, etc., he means not one of these details” (James, 1890, 472). For James this modality was referred to “the evanescent tendency of the universal,” a “too faint process” of the mind and not to an objective ‘discipline’ of generative rules seeking. It will be only a topological turn, i.e. a bestowing of meaning to space (for instance Piana’s ‘meaning woven into the figure’), what can open new perspectives.27
4 | Straddling intuition and logic
27There are no empty assumptions (i.e., assumptions without a good reason); a space that does not look like space, is not space, it is something else. As Piana repeatedly explains—allowing Husserl’s thought to emerge in all its various facets—, idealizations are never something arbitrary, but grounded in the thing.28 This aspect shuffles the cards in the game. Starting out from here, it is clear that idealization, like etceteration,29 too, will provide idealities which are not intuitive, in the ordinary sense, but not completely unrelated to intuition, either. Piana is clear on this: “around these rules and procedures [of ‘idealisation’], the contraposition between logic and intuition has too little to teach us” (NF 125), introducing in this way his original idea of a “complex dialectics between experience and conceptual formations” (NF 106).
28Diagrammatic reasoning, by straddling logic and intuition, is able to take into consideration data that might arise from the grammar of space, referring to the co-existence rules or to the following couples: inside/outside, under/over, before/after, being in the middle/or not, and so on. As Klee has taught, with the establishment of a point, an order is created inside the space: “once established, the point passes into the sphere of the order” (Piana 1979, 221) and thereby spatial relationships are revealed. Long before Klee, this was an intuition of Descartes’: letting the complex enter into a generative relationship with the simple (see above Piana’s notion of ‘generative link’, see NF 103). Hence the very idea of analysis situs comes to the fore: in a line chart, in a graph, in a genealogical tree30 or in a score—i.e., in every spatially-nested syntax with mirroring function—what counts is the position inside a network of relations, whereby each single traced line acquires meaning. As Euler, the inventor of set-theories, has already noted: “these circles, or rather these spaces [ces cercles, ou plûtot ces espaces], for it is of no importance of what figure they are of, are extremely commodious […] for unfolding all the boasted mysteries of logic” (Euler 1802, 397).
29As Husserl acknowledges in his ‘Raumbuch’: “[T]he intuitive process of geometry is actually a symbolic process. Its symbols are the figures” (Husserl 1983, 294). Husserl wrote these words probably having the following passage by Leibniz in mind: “These figures [of geometry] must also be regarded as characters, for the circle described on paper is not a true circle and need not be; it is enough that we take it for a circle” (Leibniz 1677/1989, 184). As Piana points out several times, Husserl is indebted to Leibniz, particularly via Bolzano’s Wissenschaftslehre (Piana 1988, xvi). Chess, in this sense, is a kind of geometry, that is to say: like chessmen, geometrical figures would occur in geometrical discourse not as having any particular aspect, but through the rules of the game, i.e., through the co-exact rules.31
30This parallel between chess-game and geometry can be further developed. In fact, not only is the physical aspect (of geometrical figures or pieces) equally inessential, but even their real presence. After all (as already Husserl confirmed),32 it doesn’t matter if the geometer is hallucinating or not—i.e., if the diagram really is on the blackboard or just imagined. We also find this peculiarity in the case of chess. As Piana reminds us, quoting Wittgenstein: “we agree that the movement of the wooden figures on the chessboard is something inessential” (Piana 1994, 171; Wittgen|stein/Weisman 1967, 133) and, in fact, chess-masters can play without board or pieces, just by announcing the moves, in the same way as geometricians can demonstrate their theorems just by referring to figures in their mind. This latter peculiarity allows us to state that what counts in this case, is not the mere fact that we acknowledge via intuition or via concept, but only that the geometrical domain should not lose contact with the rules of intuition.
5 | Conclusions
31As we have seen, with his idea of an internal ‘logic of the figure’—which he proudly evoked by saying that “it is we who speak of a logic of the figure” (NF 177)—Piana solves the diatribe with Hahn, revealing simplicity beneath apparent complexity and hinting to an intrinsic grammar of space. The strict dichotomy of intuition vs logic has been overcome through the notion of a syntax within space: experienced spatiality is organized according to internal rules and structures, particularly by the “display of a generative link” (NF 103). Only the generative link, in fact, could show the connection between two concepts which can appear very different (such as, for instance, a straight line and an acute angle, in the already mentioned concept of a straight angle). In the same vein, Piana’s already quoted idea of “possible dynamisms of perception” implies that the diagrammatical plan of geometrical figures has a proper grammar able to suggest the range of possible variations inside the same geometrical concept. All this supports Piana’s idea of the intrinsic dynamism of the spatial form, wrongly indicated as ‘symbol’ of staticity.
32It is in this direction that we focused on Manders: the ‘co-exact’ is a dynamic property of the geometrical figures displayed on a topological plan. In tune with articulations of lines which speak for themselves, Manders’ diagram “discipline” (2008, 96-97) introduces an objective approach that reminds us of Piana’s ways of thinking. For both, what matters is that these dynamisms are embedded into ‘the logic of the figure’, or better “woven into the figure insofar as I grasp its structure and a possibility of variation in it” (NF 122) and not into vague psychological processes of visualizations of diagrams or general concepts.33
33At the bottom line, we find the question of the shift from the particular to the general, achieved without losing contact with the empirical background. Idealization should not be fully arbitrary, in fact, losing contact with intuition would mean falling into a mere combination of symbols. It is therefore not just a matter of overcoming the contraposition of intuition vs logic—by showing that the ‘logic of figures’ and the ‘logic of propositions’ are intertwined together in the geometrical thought —but of a still deeper dichotomy. Despite Euclid having invented a completely new language game, geometry does indeed remain a ‘bastard’ science, formal and material, deductive and intuitive, because space is intrinsically a ‘bastard concept’ and the generalisation process concerning geometrical concepts follows a completely different path to, for example, that of arithmetical concepts.
34Therefore, notwithstanding his eternal fascination for figured numbers, configurations of numbers, algorithms behind geometrical figures and everything else connecting numbers and space, Piana was ready to give a negative answer to each claim that seems to bring the domain of geometrical figures close to that of numbers. In fact, he would conclude the first part of his Numero e Figura, with the following mise en garde: “Arithmetic is not at all a kind of Geometry” (NF 85). Although capable of making bold connections between different fields, Piana was equally scrupulous in “re-establishing conceptual differences once they had for some reason been removed” (NF 82). As he acknowledged, this mise en garde was none other than a clear answer to Wittgenstein: “’Is Arithmetic perhaps a kind of Geometry?’—Wittgenstein wondered. No, it is not. But the question in itself is very interesting” (NF 85).34 And I’d like to conclude with this attitude of Piana’s: to be able to grasp the intrinsic interest even in a mistaken hypothesis.
- 1 “We must therefore run the risk that our reasoning may appear bastard reasoning. Moreover, the very nature of space is a bastard one” (Piana 1988, 250), he writes, taking the expression from Plato: λογισμοì νόθοι (Timaeus, 52b). On this expression, see also Szabò (1960, 89-90).
- 2 In Piana’s Frammenti epistemologici, we read: “Spatiality has sometimes been indicated by philosophers as intrinsically static, as a true symbol of staticity, by virtue of an abstract contrast between time and space. And instead things are very different.” (Piana, 2013, 17)
- 3 With this notion of ‘diagrammatic reasoning’ I refer to the discovering of a logic of the figures, of the role of visualizing in mathematics and its reliability in proof. On this, see, among others, Giaquinto (2008), which dated the general disdain for visual thinking to 1901: “in the best books there are no figures at all” (Russell, 1918, 93) and the swing back in favour of visualization “by the late 20th century”. See, Fomenko (1994), and recent formalizations of Euclid’s diagrammatic arguments by Nathaniel Miller (2001) (‘FG’), and by John Mumma (2008) (‘Eu’). Both ‘Eu’ and ‘FG’ based Euclid’s diagrammatic inferences on topological aspects.
- 4 “In the case of Lobachevsky, the fact that at the basis of his conception there is an anti-Platonic and empirical conception of geometry is normally kept silent. […] We realize, not without some wonder, that this new foundation is being sought as a real return to experience.” (Piana 2015, 24-25)
- 5 We find this issue well expressed in Husserl’s Raumbuch (a text endorsed by Piana and whose translation appears in a book series directed by him, ‘Sensibilia’): “[I]n order to distinguish a concept from a mere and empty fiction”, we need “a continuous process” of idealization from intuition. “Idealizations are not arbitrary but, in their possibility, founded in things” (Husserl 1983, 308).
- 6 A way to ‘Euclid, the stoicheiotes’, for Piana could also have been the title given to his masterwork: The Elements, and, therefore, the shift made from a material primum (like ‘water’ and ‘fire’) to a conceptual primum (lines and points). It is no coincidence that one of Piana’s titles is: ‘Elements’ of a Doctrine of Experience.
- 7 By ‘experimented spatiality’ is actually meant “a multiplicity of spaces related to different ways of possible experiences” (NF 120).
- 8 “Between the logic of the figures and the logic of the propositions, which are intertwined together in the geometrical thought, it is up to the thought itself to decide whether, at a certain point, to give priority either to the latter or to the former” (NF 123-124). Despite the stressing on this peculiar logic of figures, Piana warns against ‘Schopenhauer’s mistake’, that is: “To settle himself for the figures as if the logic of the figure were everything, and the logic of the proposition nothing!” (NF 126-127). On this, see the whole § 15 of the first volume of The world as will and representation (Schopenhauer 1969, 69-83).
- 9 “In order to raise the suspicion that, despite their obvious and superficial validity, those comments—which hasten to present the Euclidean definitions as ‘intuitive’ residues, that advanced thought will finally be able to put aside as dross still waiting to be passed through a finer and more subtle filter—are misleading” (NF 105). “Equally unsatisfactory is another position that apparently moves in the opposite direction to the Euclidean definitions. […] In reality, this line of discourse already targets the idea that [...] geometry in general, Euclidean or non-Euclidean, [...] generally deals with ‘logic’, and not with ‘intuition’.” (NF 105)
- 10 The term ‘structure’, which Piana uses in the quote, is very important for a genetical interpretation of geometry and, referring to an articulation and an internal way of constitution, is very meaningful in Piana’s thought. He even proposed to translate Wesen (in Husserl’s Logical Investigations) with ‘structure’, rather than ‘essence’ (but Enzo Paci opted for a more standard translation). Piana, however, used to speak of ‘phenomenological structuralism’.
- 11 Concerning this idea of a geometrical ‘impossibility’, see Wittgenstein (1975, 24, 141).
- 12 Piana refers here to the paradoxical notion of a ‘straight angle’ and notes how “a straight line and an acute angle actually look very different”, but if one follows the rule of the generative link, the connection between the two concepts becomes clear.
- 13 Hahn (1980). On the same subject Piana refers to Volkert (1986).
- 14 Strong constructivist interpretations of geometry can lead to see geometry as an intrinsically subjective activity, Piana refers rather to a generative interpretation, as the simple and recursive apply of an algorithm.
- 15 Hahn went so far to declare: “[I]t is not true, as Kant urged, that intuition is a pure a priori means of knowledge, but rather that it is force of habit rooted in psychological inertia” (Hahn 1980, 101). “If the use of multi-dimensional and non-Euclidean geometries for the ordering of our experience continues to prove itself so that we become more and more accustomed to dealing with these logical constructs; if they penetrate into the curriculum of the schools, if we, so to speak, learn them at our mother's knee, as we now learn three-dimensional Euclidean geometry, then nobody will think of saying that these geometries are contrary to intuition.” (Hahn 1980, 101)
- 16 After Leibniz, Lambert, too, investigates the realm of a spatially-nested syntax, reaching the point where “figures are, so to speak, transformed into signs and lines drawn acquire meaning” (Lambert, 1770/1965b, 521). Only an organized space can establish whether or not it is possible to conjoin three sides, excluding such chimeras as a “dreamed” triangle with “equal sides and unequal angles” (Lambert 1764/1965a, 524).
- 17 “Es genüge gezeigt zu haben, dass die Logik nirgend sonst festen Boden findet, als in den Gesetzen, welche aus der Betrachtung des Raumes hervorgehn” (Lange 1877, 145); see infra, footnote 28.
- 18 ‘Eu’ by John Mumma also specifies a procedure for interpreting a constructed diagram in terms of the way it was constructed.
- 19 This can recall the way how Husserl described geometric essences as invariants through different types of free variations. Despite the deep differences between exact and descriptive sciences, Husserl have to admit that the mathematician also “employs the variation of figures in phantasy,” though “only when he devises a reasoning or when he produces the differences of the possible cases”, and never “for the demonstrations” (Husserl, Ms. K I 33: 97a, quoted in Caracciolo, 2017, 109). As germination of the idea of ‘variation’ in Husserl, Caracciolo quoted also Klein’s ‘Erlangen Program’ and the hierarchy of invariants. On eidetic variation in geometry see, among others: Tieszen (2005), where it is mentioned how “Husserl’s ideas about Wesenanalyse influenced Carnap in his 1922 thesis on space” (Tieszen 2005, 154). Carnap’s idea of ‘structure’ and his “logical foundation of knowledge of intuitive space” (Carnap 1922, 22) seem relevant within this discourse on space.
- 20 For this Husserlian notion, see Piana (2013). Completely unknown to Kant, this notion is for Piana the keystone for a philosophy of experience. If ‘synthesis’ is normally understood as an activity of the subject, ‘passive synthesis’—on the contrary—designates the autonomous organization of sensible contents, in which the subject is passively involved.
- 21 Manders emphasizes how the Greek word for figure itself, ‘schema’, referred to a ‘shaped region’ (see Manders 2008, 90). Proclus, for instance, accepts a four-sided triangle (Proclus 1992, 329 [416]). In the genesis of some diagrams—for instance that of two intersecting figures—we know already that there must be an intersection point, no matter how big or small or deformed or shifted the circles are.
- 22 His theory aims to overcome the several criticisms that arose at the beginning of the 19th century, concerning the imperfection, atypicality or intrinsic individuality of diagrams in geometry.
- 23 A well-known case is ‘the all-triangles-are-isosceles argument’. This fallacy is a proof by contradiction and the problem is that the perpendicular and the bisector do not intersect inside the triangle as the figure erroneously suggests. Therefore, an intervention on the discursive plane is required, with explicit claims concerning the outcome of constructions.
- 24 “A lettering scheme facilitates cross-references to the diagram” (Manders 2008, 86). For him, the mere existence of “diagrammatically intractable geometricals, such as space-filling curves or general Riemannian geometries” is not enough to undermine the use of diagrams in Euclidean geometry.
- 25 “Geometrical constructions are in general only quasi-determinate: adding elements to a diagram by a prescribed construction may yield finitely many diagrams from any given initial diagram, rather than just one.” (Manders 2008, 102)
- 26 In the Introduction (§ 13) to his Principle of Human Knowledge, Berkeley—quoting a passage of Lockes’s Essay (book IV, sect. vii, ch. 9)—shows the intrinsic impossibility to really think an idea that fits such description (Berkeley 1710/1948,51). How this could be a misinterpretation of Locke, see Aaron (1932, 173-176).
- 27 In his (published posthumously by Cohen) Logische Studien, Friedrick Albert Lange aimed to reduce the logical truth to what is representable in spatial terms: “we believe in the principle that the whole is greater than the part, or that equals added to equals yield equals, because we see these principles embodied into spatial figures. The same is true of the law of non-contradiction: in a spatial image of some sort [Raumbilde irgend welcher Art], be it in a concrete case or in a mere linear schema [Linienschema], we see [sehen wir] that I cannot affirm and deny the same of the same objects” (Lange 1877, 28-29). For Peirce, the entire domain of necessary reasoning—that is, mathematics and deductive logic—is diagrammatic, i.e. constructive in the Kantian sense; this shift was inspired, as Peirce himself acknowledged, by Lange’s doctrine.
- 28 As already noted, this aspect was a topos in Husserl’s considerations (see footnote 6 on Husserl’s Raumbuch): “Die Figuren der Geometrie sind allerdings, sofern sie ideale sind, selbst geschaffene Objekte: aber cum fundamentum in rebus” (Husserl, Ms. K I 33: 99b, quoted in Caracciolo, 2017).
- 29 On etceteration as examples of ‘intellectual syntheses’, see Piana (1979).
- 30 It is no coincidence that Piana quotes the ‘genealogical tree’ proposed by Leibniz in his fifth letter to Clarke (Piana 2015, 35; Leibniz 1956, 70-71). The analysis situs is equally an expression of space conceived as an order of coexistence.
- 31 See, Husserl’s “certain operation-meaning or game-meaning” (Husserl 2001, 211) outlined in the § 20 of the ‘First logical Investigation’: “Chessmen are not part of the chess-game as bits of ivory and wood having such and such shapes and colours. Their phenomenal and physical constitution is quite indifferent and can be varied at will. They become chessmen, counters in the chess-game, through the game’s rules which give them their fixed games-meaning” (Husserl 2001, 210). Here, Husserl quotes Lambert, a philosopher familiar to Leibniz’s work on characteristic signs. It is interesting the leading role of a ‘spatial model’ of thought in authors read by Husserl during his studies, in particular Lotze’s Localzeichen and Stumpf’s Raumvorstellung.
- 32 “The geometer who draws his figures on the board produces thereby factually existing lines on the factually existing board. But his experiencing of the product, qua experiencing, no more grounds his geometrical seeing of essences and eidetic thinking than does his physical producing. This is why it does not matter whether his experiencing is hallucination or whether, instead of actually drawing his lines and constructions, he imagines them in a world of phantasy.” (Husserl 1983, 16)
- 33 The mathematization of logic presupposes, in fact, abandoning the introspective approaches which could be at the basis of the already mentioned vague notion of ‘general concepts’ as: impossible ideas formed by putting together inconsistent aspects.
- 34 This seems a clear position against a formalisation or arithmetization of geometry. Wittgenstein in his Philosophical Remarks: “You could say Arithmetic is a kind of Geometry, i.e. what in Geometry are constructions on paper, in Arithmetic are calculations (on paper). You could say it is a more general kind of Geometry” (Wittgenstein 1975, 131). In a successive Remark, Wittgenstein sharpens his point: “[T]he point of the remark that Arithmetic is a kind of Geometry is simply that arithmetical constructions are autonomous like geometrical ones, and hence so to speak, themselves guarantee their applicability” (Wittgenstein 1975,132).